Beregning af kabeltværsnit efter strøm og strøm: hvordan man korrekt beregner ledninger

Planlægger du at gøre modernisering af elnettet eller forlænge strømledningen til køkkenet for at tilslutte et nyt elektrisk komfur? Her vil minimal viden om lederens tværsnit og denne parameters effekt på effekt og strøm være nyttig.

Enig i, at forkert beregning af kabeltværsnittet fører til overophedning og kortslutning eller til uberettigede omkostninger.

Det er meget vigtigt at udføre beregninger på designstadiet, da fejl skjulte ledninger og efterfølgende udskiftning er forbundet med betydelige omkostninger. Vi hjælper dig med at forstå forviklingerne ved beregninger for at undgå problemer i den videre drift af elektriske netværk.

For ikke at belaste dig med komplekse beregninger, har vi udvalgt klare formler og beregningsmuligheder, præsenteret oplysningerne i en tilgængelig form og forsynet formlerne med forklaringer. Tematiske fotos og videomaterialer er også blevet tilføjet til artiklen, så du tydeligt kan forstå essensen af ​​det emne, der overvejes.

Beregning af tværsnit for forbrugerkraft

Hovedformålet med ledere er at levere elektrisk energi til forbrugerne i den nødvendige mængde. Da superledere ikke er tilgængelige under normale driftsforhold, skal der tages hensyn til ledermaterialets modstand.

Beregning af det nødvendige afsnit ledere og kabler afhængigt af den samlede effekt af forbrugerne er baseret på langsigtet driftserfaring.

Lad os begynde det generelle forløb med beregninger ved først at udføre beregninger ved hjælp af formlen:

P = (P1+P2+..PN)*K*J,

Hvor:

• P – strømmen af ​​alle forbrugere tilsluttet den beregnede filial i watt.
• P1, P2, PN – effekt af henholdsvis den første, anden, n. forbruger i watt.

Efter at have modtaget resultatet i slutningen af ​​beregningerne ved hjælp af ovenstående formel, var det tid til at vende sig til tabeldataene.

Nu skal du vælge det ønskede afsnit i henhold til tabel 1.

Tabel 1. Trådtværsnittet skal altid vælges til nærmeste større side (+)

Trin #1 - beregning af reaktiv og aktiv effekt

Forbrugerkapacitet er angivet i udstyrsdokumenterne. Typisk angiver udstyrsdatablade aktiv effekt sammen med reaktiv effekt.

Enheder med en aktiv type belastning konverterer al modtaget elektrisk energi, under hensyntagen til effektivitet, til nyttigt arbejde: mekanisk, termisk eller en anden type.

Enheder med aktiv belastning omfatter glødelamper, varmelegemer og elektriske komfurer.

For sådanne enheder har beregningen af ​​strøm efter strøm og spænding formen:

P=U*I,

Hvor:

• P – effekt i W;
• U – spænding i V;
• jeg – strømstyrke i A.

Enheder med en reaktiv type belastning er i stand til at akkumulere energi fra en kilde og derefter returnere den. Denne udveksling sker på grund af forskydningen af ​​den nuværende sinusoid og spændings sinusoid.

Ved nulfaseforskydning har effekt P=U*I altid en positiv værdi. Enheder med en aktiv type belastning har en sådan graf over faserne af strøm og spænding (I, i - strøm, U, u - spænding, π - pi lig med 3,14)

Enheder med reaktiv effekt omfatter elektriske motorer, elektroniske enheder af alle størrelser og formål og transformere.

Når der er et faseskift mellem strømsinus og spændingssinus, kan effekten P=U*I være negativ (I, i - strøm, U, u - spænding, π - pi lig med 3,14). En enhed med reaktiv effekt returnerer lagret energi tilbage til kilden

Elektriske netværk er bygget på en sådan måde, at de kan overføre elektrisk energi i én retning fra kilde til belastning.

Derfor er den returnerede energi fra en forbruger med en reaktiv belastning parasitisk og spildes på opvarmning af ledere og andre komponenter.

Reaktiv effekt afhænger af fasevinklen mellem spændings- og strømsinusformerne. Faseforskydningsvinklen udtrykkes gennem cosφ.

For at finde den samlede effekt, brug formlen:

P = Q / cosφ,

Hvor Q – reaktiv effekt i VAR.

Typisk angiver enhedens datablad reaktiv effekt og cosφ.

Eksempel: passet til borehammeren angiver en reaktiv effekt på 1200 VAr og cosφ = 0,7.Derfor vil det samlede strømforbrug være lig med:

P = 1200/0,7 = 1714 W

Hvis cosφ ikke kunne findes, kan cosφ for langt de fleste elektriske husholdningsapparater tages lig med 0,7.

Trin #2 - søg efter simultanitet og marginkoefficienter

K – dimensionsløs simultanitetskoefficient, viser hvor mange forbrugere der kan tilsluttes netværket på samme tid. Det sker sjældent, at alle enheder bruger strøm på samme tid.

Samtidig drift af tv'et og musikcentret er usandsynligt. Fra etableret praksis kan K tages lig med 0,8. Hvis du planlægger at bruge alle forbrugere samtidigt, skal K indstilles til 1.

J – dimensionsløs sikkerhedsfaktor. Karakteriserer oprettelsen af ​​en strømreserve for fremtidige forbrugere.

Fremskridt står ikke stille; hvert år opfindes nye fantastiske og nyttige elektriske enheder. Elforbruget forventes at stige med 84 % i 2050. Typisk tages J til at være mellem 1,5 og 2,0.

Trin #3 - udførelse af beregninger ved hjælp af den geometriske metode

I alle elektriske beregninger tages lederens tværsnitsareal - kernens tværsnit. Målt i mm².

Det er ofte nødvendigt at lære, hvordan man regner korrekt tråd diameter leder ledninger.

I dette tilfælde er der en simpel geometrisk formel for en monolitisk rund ledning:

S = π*R² = π*D²/4, eller omvendt

D = √(4*S / π)

For rektangulære ledere:

S = h * m,

Hvor:

• S – kerneareal i mm²;
• R – kerneradius i mm;
• D – kernediameter i mm;
• h, m – henholdsvis bredde og højde i mm;
• π — pi er lig med 3,14.

Hvis du køber en snoet ledning, hvor en leder består af mange snoede ledninger med rundt tværsnit, udføres beregningen i henhold til formlen:

S = N*D²/1,27,

Hvor N – antal ledninger i kernen.

Ledninger med kerner snoet fra flere ledninger har generelt bedre ledningsevne end monolitiske. Dette skyldes de særlige forhold ved strømgennemstrømning gennem en leder med et rundt tværsnit.

Elektrisk strøm er bevægelsen af ​​lignende ladninger langs en leder. Ligesom ladninger frastøder hinanden, så forskydes ladningsfordelingstætheden mod lederens overflade.

En anden fordel ved strandede ledninger er deres fleksibilitet og mekaniske modstand. Monolitiske ledninger er billigere og bruges hovedsageligt til stationær installation.

Trin #4—beregn effekttværsnittet i praksis

Opgave: den samlede effekt af forbrugere i køkkenet er 5000 W (hvilket betyder, at effekten af ​​alle reaktive forbrugere er blevet genberegnet). Alle forbrugere er tilsluttet et 1-faset 220 V netværk og får strøm fra én gren.

Tabel 2. Hvis du planlægger at tilslutte yderligere forbrugere i fremtiden, viser tabellen den nødvendige effekt af almindelige husholdningsapparater (+)

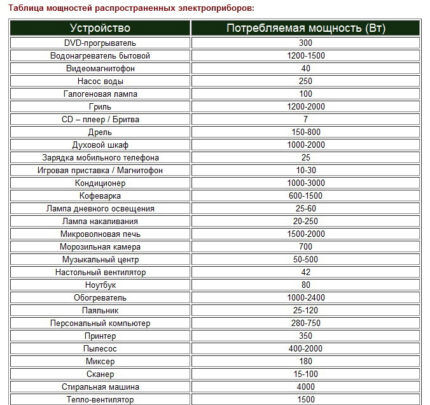
Løsning:

Lad os tage simultanitetskoefficienten K lig med 0,8. Køkkenet er et sted for konstant innovation, man ved aldrig, sikkerhedsfaktoren er J=2,0. Den samlede estimerede effekt vil være:

P = 5000*0,8*2 = 8000 W = 8 kW

Ved hjælp af værdien af ​​den beregnede effekt ser vi efter den nærmeste værdi i tabel 1.

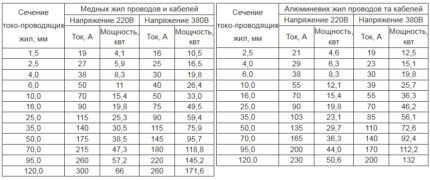
Det nærmeste egnede kernetværsnit til et enfaset netværk er en kobberleder med et tværsnit på 4 mm². Lignende ledningsstørrelse med 6 mm aluminiumskerne².

For enkeltlederledninger vil minimumsdiameteren være henholdsvis 2,3 mm og 2,8 mm.Ved anvendelse af en multi-core mulighed opsummeres tværsnittet af de enkelte kerner.

Beregning af aktuelt tværsnit

Beregninger af det nødvendige strøm- og effekttværsnit af kabler og ledninger vil give mere nøjagtige resultater.Sådanne beregninger gør det muligt at evaluere den overordnede indflydelse af forskellige faktorer på ledere, herunder termisk belastning, mærke af ledninger, type lægning, driftsforhold osv.

Hele beregningen udføres i følgende trin:

• valg af magt for alle forbrugere;
• beregning af strømme, der passerer gennem en leder;
• valg af et passende tværsnit ved hjælp af tabeller.

For denne beregningsmulighed tages forbrugernes effekt i form af strøm og spænding uden at tage højde for korrektionsfaktorer. De vil blive taget i betragtning, når den nuværende styrke summeres.

Trin #1 - beregning af strømstyrke ved hjælp af formler

For dem, der har glemt skolens fysikkursus, tilbyder vi de grundlæggende formler i form af et grafisk diagram som et visuelt snydeark:

Det "klassiske hjul" demonstrerer klart forholdet mellem formler og den indbyrdes afhængighed af egenskaberne ved elektrisk strøm (I - strømstyrke, P - effekt, U - spænding, R - kerneradius)

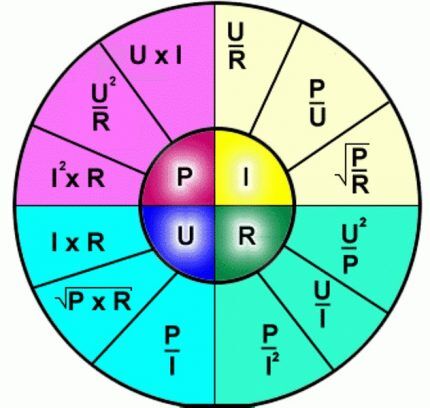
Lad os nedskrive afhængigheden af ​​strømmen I af effekten P og linjespændingen U:

I = P/U_l,

Hvor:

• jeg — strømstyrke, taget i ampere;
• P — effekt i watt;
• U_l — netspænding i volt.

Netspændingen afhænger generelt af strømforsyningskilden; den kan være en- eller trefaset.

Forholdet mellem lineær og fasespænding:

1. U_l = U*cosφ i tilfælde af enfaset spænding.
2. U_l = U*√3*cosφ i tilfælde af trefaset spænding.

For husholdningselektriske forbrugere accepteres cosφ=1, så den lineære spænding kan omskrives:

1. U_l = 220 V for enfaset spænding.
2. U_l = 380 V for trefaset spænding.

Dernæst opsummerer vi alle forbrugte strømme ved hjælp af formlen:

I = (I1+I2+…IN)*K*J,

Hvor:

• jeg – samlet strøm i ampere;
• I1..IN – strømstyrken for hver forbruger i ampere;
• K – simultanitetskoefficient;
• J – sikkerhedsfaktor.

Koefficienterne K og J har samme værdier som dem, der bruges ved beregning af den samlede effekt.

Der kan være et tilfælde, når der i et trefaset netværk strømmer en strøm af ulige styrke gennem forskellige faseledere.

Dette sker, når enfasede og trefasede forbrugere tilsluttes et trefaset kabel på samme tid. For eksempel strømforsynes en trefaset maskine og enfaset belysning.

Et naturligt spørgsmål opstår: hvordan beregnes tværsnittet af en trådet tråd i sådanne tilfælde? Svaret er enkelt - beregninger er lavet ud fra den mest belastede kerne.

Trin #2 - udvælgelse af en passende sektion ved hjælp af tabeller

Driftsreglerne for elektriske installationer (PEU) indeholder en række tabeller til valg af det nødvendige tværsnit af kabelkernen.

En leders ledningsevne afhænger af temperaturen. For metalledere stiger modstanden med stigende temperatur.

Når en vis tærskel overskrides, bliver processen selvbærende: Jo højere modstand, jo højere temperatur, jo højere modstand osv. indtil lederen brænder ud eller forårsager kortslutning.

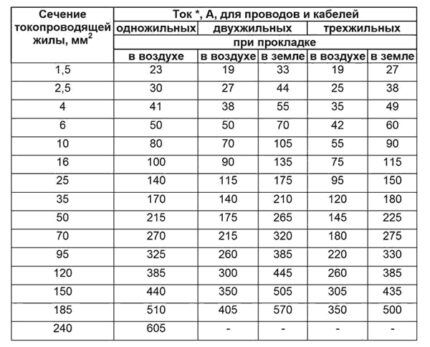
De næste to tabeller (3 og 4) viser ledernes tværsnit afhængig af strømme og installationsmetode.

Tabel 3. Først skal du vælge metoden til at lægge ledningerne, dette bestemmer hvor effektiv kølingen er (+)

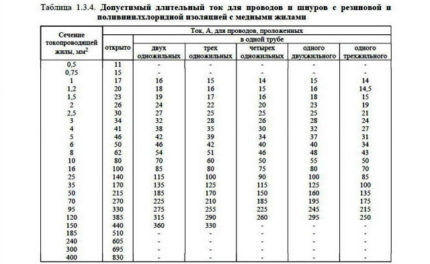
Et kabel adskiller sig fra en ledning ved, at alle kabelkerner, udstyret med deres egen isolering, er snoet til et bundt og omsluttet af en fælles isoleringskappe. Flere detaljer om forskellene og typerne af kabelprodukter er skrevet i dette artikel.

Tabel 4. Den åbne metode er angivet for alle ledertværsnitsværdier, dog i praksis lægges sektioner under 3 mm2 ikke åbent af hensyn til mekanisk styrke (+)

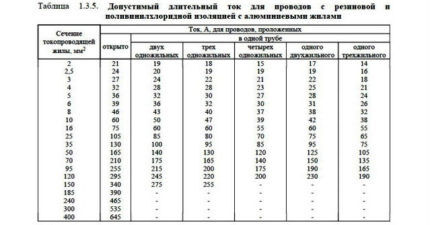
Ved brug af tabeller anvendes følgende koefficienter på den tilladte kontinuerlige strøm:

• 0,68 hvis 5-6 kerner;
• 0,63 hvis 7-9 kerner;
• 0,6 hvis 10-12 kerner.

Reduktionsfaktorer anvendes på aktuelle værdier fra kolonnen "åben".

Nul- og jordlederne er ikke inkluderet i antallet af ledere.

I henhold til PES-standarder foretages valget af tværsnittet af nullederen i henhold til den tilladte kontinuerlige strøm som mindst 50% af faselederen.

De næste to tabeller (5 og 6) viser afhængigheden af ​​den tilladte langtidsstrøm, når den lægges i jorden.

Tabel 5. Afhængigheder af tilladt langtidsstrøm for kobberkabler, når de er lagt i luft eller jord

Den aktuelle belastning er forskellig, når den lægges åbent, og når den lægges dybt ned i jorden. De accepteres som lige, hvis lægning i jorden udføres ved hjælp af bakker.

Tabel 6. Afhængigheder af tilladt kontinuerlig strøm for aluminiumskabler, når de er lagt i luft eller jord

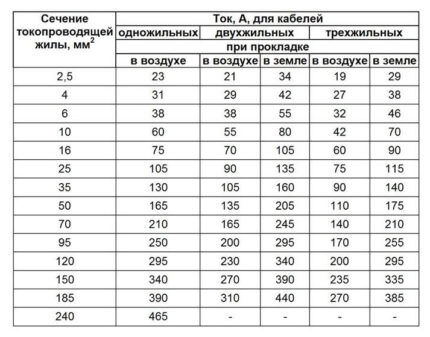
For installation af midlertidige strømforsyningsledninger (bærende, hvis til privat brug), gælder følgende tabel (7).

Tabel 7. Tilladt kontinuerlig strøm ved brug af bærbare slangeledninger, bærbare slange- og skaktabler, projektørkabler, fleksible bærbare ledninger. Der anvendes kun kobberledere

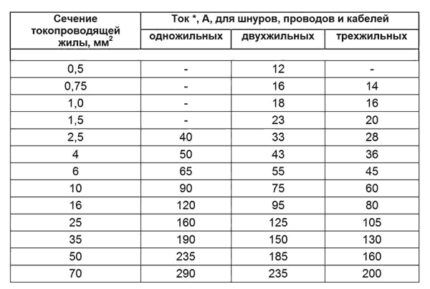
Når du lægger kabler i jorden, er det ud over varmeafledningsegenskaberne nødvendigt at tage hensyn til modstanden, hvilket afspejles i følgende tabel (8):

Tabel 8. Korrektionsfaktor afhængig af jordens type og resistivitet for den tilladte langtidsstrøm, ved beregning af kabeltværsnittet (+)

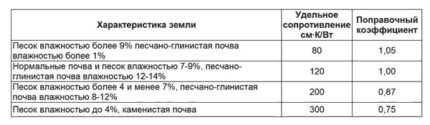
Beregning og valg af kobberkerner op til 6 mm² eller aluminium op til 10 mm² udføres som for kontinuerlig strøm.

Ved store tværsnit er det muligt at anvende en reduktionsfaktor:

0,875 * √T_pv

Hvor T_pv — forholdet mellem koblingsvarighed og cyklusvarighed.

Varigheden af ​​at tænde antages at være højst 4 minutter. I dette tilfælde bør cyklussen ikke overstige 10 minutter.

Ved valg af kabel til distribution af el ind træhus Der lægges særlig vægt på dens brandmodstand.

Trin #3 - beregning af det aktuelle tværsnit af lederen ved hjælp af et eksempel

Opgave: beregn det nødvendige afsnit kobberkabel til tilslutning:

• trefaset træbearbejdningsmaskine med en effekt på 4000 W;
• trefaset svejsemaskine med en effekt på 6000 W;
• husholdningsapparater i huset med en samlet effekt på 25.000 W;

Forbindelsen vil blive lavet med et fem-leder kabel (tre faseledere, en neutral og en jording), lagt i jorden.

Isoleringen af ​​kabel- og ledningsprodukter beregnes for en bestemt driftsspænding. Det skal tages i betragtning, at driftsspændingen for hans produkt angivet af producenten skal være højere end netspændingen

Løsning.

Trin 1. Vi beregner den lineære spænding af en trefaset forbindelse:

U_l = 220 * √3 = 380 V

Trin #2. Husholdningsapparater, en værktøjsmaskine og en svejsemaskine har reaktiv effekt, så maskinens og udstyrets kraft vil være:

P_{de der} = 25000 / 0,7 = 35700 W

P_obor = 10000 / 0,7 = 14300 W

Trin #3. Strøm påkrævet for at tilslutte husholdningsapparater:

jeg_{de der} = 35700 / 220 = 162 A

Trin #4. Strøm påkrævet for at tilslutte udstyr:

jeg_obor = 14300 / 380 = 38 A

Trin #5. Den nødvendige strøm til tilslutning af husholdningsapparater beregnes ud fra en fase. Ifølge problemet er der tre faser. Derfor kan strømmen fordeles mellem faserne. For nemheds skyld antager vi en ensartet fordeling:

jeg_{de der} = 162 / 3 = 54 A

Trin #6. Strøm pr. fase:

jeg_f = 38 + 54 = 92 A

Trin #7. Udstyr og husholdningsapparater vil ikke virke samtidig, derudover afsætter vi en reserve på 1,5. Efter anvendelse af korrektionsfaktorer:

jeg_f = 92 * 1,5 * 0,8 = 110 A

Trin #8. Selvom kablet indeholder 5 ledere, tages der kun hensyn til trefasede ledere. Ifølge tabel 8 i kolonnen trelederkabel i jorden finder vi, at en strøm på 115 A svarer til et lederetværsnit på 16 mm².

Trin #9. I henhold til tabel 8 anvender vi en korrektionsfaktor afhængig af jordens karakteristika. For en normal jordtype er koefficienten 1.

Trin #10. Beregn eventuelt kernens diameter:

D = √(4*16 / 3,14) = 4,5 mm

Hvis beregningen kun blev foretaget baseret på strøm, uden at tage højde for de særlige forhold ved kabellægning, ville kernens tværsnit være 25 mm². Beregning af strømstyrke er mere kompliceret, men giver dig nogle gange mulighed for at spare betydelige penge, især når det kommer til multi-core strømkabler.

Du kan læse mere om sammenhængen mellem spændings- og strømværdier her.

Beregning af spændingsfald

Enhver leder, undtagen superledere, har modstand. Hvis kablet eller ledningen er lang nok, opstår der derfor et spændingsfald.

PES-standarder kræver, at kabelkernens tværsnit er således, at spændingsfaldet ikke er mere end 5 %.

Tabel 9. Resistivitet af almindelige metalledere (+)

Det drejer sig primært om lavspændingskabler med lille tværsnit.

Spændingsfaldsberegningen er som følger:

R = 2*(ρ *L)/S,

U_pude = I * R,

U_% = (U_pude /u_lin) * 100,

Hvor:

• 2 - koefficient på grund af det faktum, at strømmen nødvendigvis løber gennem to ledninger;
• R – ledermodstand, Ohm;
• ρ — lederresistivitet, Ohm*mm²/m;
• S – ledertværsnit, mm²;
• U_pude – faldspænding, V;
• U_% - spændingsfald i forhold til U_lin,%.

Ved hjælp af formler kan du selvstændigt udføre de nødvendige beregninger.

Bærende regneeksempel

Opgave: beregn spændingsfaldet for en kobbertråd med et tværsnit af en kerne på 1,5 mm². Ledningen er påkrævet for at forbinde en enfaset elektrisk svejsemaskine med en samlet effekt på 7 kW. Trådlængde 20 m.

De, der ønsker at tilslutte en husholdningssvejsemaskine til en elektrisk netværksgren, bør tage hensyn til den strømsigte, som det anvendte kabel er designet til. Det er muligt, at den samlede effekt af betjeningsenheder kan være højere. Den bedste mulighed er at forbinde forbrugere til separate filialer

Løsning:

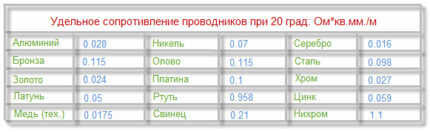
Trin 1. Vi beregner modstanden af ​​kobbertråden ved hjælp af tabel 9:

R = 2*(0,0175 * 20) / 1,5 = 0,47 Ohm

Trin #2. Strøm, der løber gennem lederen:

I = 7000 / 220 = 31,8 A

Trin #3. Spændingsfald på ledningen:

U_pude = 31,8 * 0,47 = 14,95 V

Trin #4. Vi beregner procentdelen af ​​spændingsfald:

U_% = (14,95 / 220) * 100 = 6,8%

Konklusion: For at forbinde svejsemaskinen kræves en leder med et stort tværsnit.

Konklusioner og nyttig video om emnet

Beregning af ledertværsnittet ved hjælp af formlerne:

Anbefalinger fra specialister om valg af kabel- og ledningsprodukter:

Ovenstående beregninger gælder for kobber- og aluminiumsledere til industriel brug. For andre typer ledere er den samlede varmeoverførsel forudberegnet.

Baseret på disse data beregnes den maksimale strøm, der kan strømme gennem lederen uden at forårsage for kraftig opvarmning.

Hvis du har spørgsmål om metoden til beregning af kabeltværsnittet eller gerne vil dele din personlige erfaring, bedes du skrive kommentarer til denne artikel.Gennemgangssektionen er placeret nedenfor.