Ohms lov for en komplet kæde og for en del af en kæde: muligheder for at skrive formlen, beskrivelse og forklaring

Der er ingen måde for en professionel elektriker eller elektronikspecialist at omgå Ohms lov i sine egne aktiviteter og løse eventuelle problemer relateret til opsætning, justering og reparation af elektroniske og elektriske kredsløb.

Faktisk skal alle forstå denne lov. For alle skal forholde sig til el i hverdagen.

Og selvom den tyske fysiker Ohms lov er fastsat i gymnasiets læseplan, bliver den i praksis ikke altid studeret rettidigt. Derfor vil vi i vores materiale overveje et sådant relevant emne for livet og forstå mulighederne for at skrive formlen.

Enkeltsektion og komplet elektrisk kredsløb

I betragtning af et elektrisk kredsløb ud fra synspunktet om at anvende Ohms lov til et kredsløb, skal der bemærkes to mulige beregningsmuligheder: for en separat sektion og for et fuldgyldigt kredsløb.

Beregning af strømmen af ​​en elektrisk kredsløbssektion

En sektion af et elektrisk kredsløb anses som regel for at være den del af kredsløbet, der udelukker kilden til EMF, som havende yderligere intern modstand.

Derfor ser beregningsformlen i dette tilfælde enkel ud:

I = U/R,

Hvor henholdsvis:

• jeg – strømstyrke;
• U – påført spænding;
• R - modstand.

Fortolkningen af ​​formlen er enkel - strømmen, der strømmer gennem en bestemt sektion af kredsløbet, er proportional med den spænding, der påføres den, og modstanden er omvendt proportional.

Den såkaldte grafiske "daisy", hvorigennem hele sættet af variationer af formuleringer baseret på Ohms lov præsenteres. Praktisk værktøj til lommeopbevaring: sektor "P" - effektformler; sektor "U" - spændingsformler; sektor "I" - nuværende formler; sektor "R" - modstandsformler

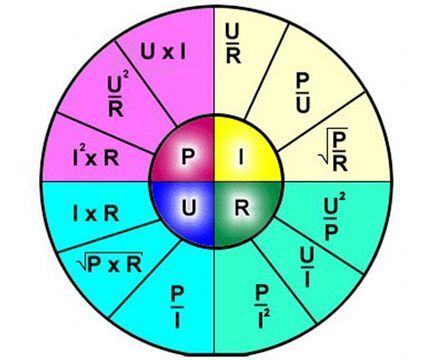
Således beskriver formlen klart afhængigheden af ​​strømstrømmen gennem en separat sektion af det elektriske kredsløb i forhold til visse værdier af spænding og modstand.

Formlen er praktisk at bruge, for eksempel ved beregning af parametrene for den modstand, der skal loddes ind i kredsløbet, hvis spændingen og strømmen er givet.

Ohms lov og to konsekvenser, som enhver professionel elektromekanisk ingeniør, elektroingeniør, elektronikingeniør og enhver, der er involveret i driften af ​​elektriske kredsløb, skal kende. Fra venstre mod højre: 1 - strømbestemmelse; 2 - bestemmelse af modstand; 3 - definition af spænding, hvor I - strøm, U - spænding, R - modstand

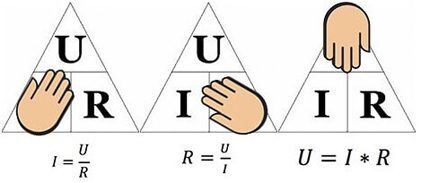
Ovenstående figur vil hjælpe med at bestemme, for eksempel, strømmen, der flyder gennem en 10-ohm modstand, til hvilken der påføres en spænding på 12 volt. Ved at erstatte værdierne finder vi – I = 12 / 10 = 1,2 ampere.

Problemerne med at finde modstand (når strøm og spænding er kendt) eller spænding (når spænding og strøm er kendt) løses på lignende måde.

Du kan således altid vælge den nødvendige driftsspænding, den nødvendige strømstyrke og det optimale modstandselement.

Formlen, der foreslås brugt, kræver ikke, at der tages hensyn til spændingskildens parametre.Et kredsløb, der for eksempel indeholder et batteri, vil dog blive beregnet ved hjælp af en anden formel. I diagrammet: A – tænde for amperemeteret; V – tænd for voltmeteret.

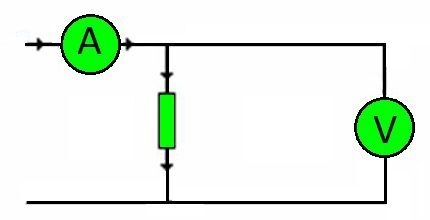
Forresten er forbindelsesledningerne til ethvert kredsløb modstande. Mængden af ​​belastning, de skal bære, bestemmes af spændingen.

I overensstemmelse hermed, igen ved hjælp af Ohms lov, bliver det muligt nøjagtigt at vælge det nødvendige ledertværsnit, afhængigt af kernematerialet.

Vi har detaljerede instruktioner på vores hjemmeside kabeltværsnitsberegning med hensyn til strøm og strøm.

Beregningsmulighed for en komplet kæde

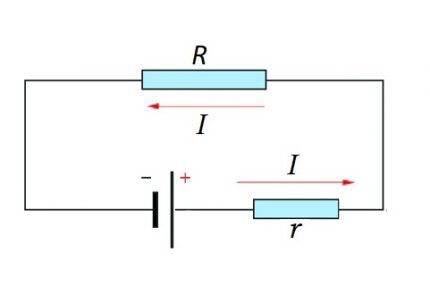
Et komplet kredsløb består af en sektion (sektioner) samt en kilde til EMF. Det vil sige, at den interne modstand af EMF-kilden føjes til den eksisterende resistive komponent i kredsløbssektionen.

Derfor er det logisk at ændre ovenstående formel lidt:

I = U / (R + r)

Selvfølgelig kan værdien af ​​den interne modstand af EMF i Ohms lov for et komplet elektrisk kredsløb betragtes som ubetydelig, selvom denne modstandsværdi i høj grad afhænger af strukturen af ​​EMF-kilden.

Men ved beregning af komplekse elektroniske kredsløb, elektriske kredsløb med mange ledere, er tilstedeværelsen af ​​yderligere modstand en vigtig faktor.

Ved beregninger under betingelser for et komplet elektrisk kredsløb tages der altid hensyn til EMF-kildens resistive værdi. Denne værdi summeres med den resistive modstand af selve det elektriske kredsløb. I diagrammet: I - strømflow; R—eksternt modstandselement; r er den resistive faktor for EMF (energikilden)

Både for en sektion af et kredsløb og for et komplet kredsløb skal det naturlige moment tages i betragtning - brugen af ​​konstant eller variabel strøm.

Hvis de punkter, der er nævnt ovenfor, karakteristiske for Ohms lov, blev betragtet ud fra synspunktet om at bruge jævnstrøm, ser alt derfor noget anderledes ud med vekselstrøm.

Overvejelse af lovens effekt på en variabel mængde

Begrebet "modstand" over for betingelserne for at passere vekselstrøm bør betragtes mere som begrebet "impedans". Dette refererer til kombinationen af ​​en resistiv belastning (Ra) og en reaktiv modstandsbelastning (Rr).

Sådanne fænomener er forårsaget af parametrene for induktive elementer og lovene om at skifte i forhold til en variabel spændingsværdi - en sinusformet strømværdi.

Dette er det ækvivalente kredsløb af et elektrisk vekselstrømkredsløb til beregning ved hjælp af formuleringer baseret på principperne i Ohms lov: R - modstandskomponent; C er den kapacitive komponent; L—induktiv komponent; EMF er en energikilde; I - strømflow

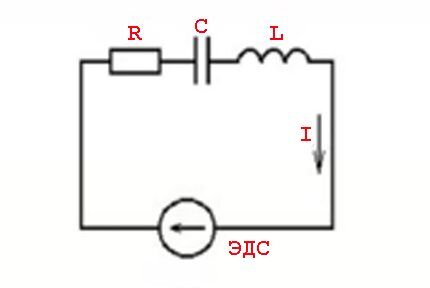
Med andre ord er der en effekt af strømværdier, der fører (lag) fra spændingsværdier, som er ledsaget af fremkomsten af ​​aktive (resistive) og reaktive (induktive eller kapacitive) kræfter.

Sådanne fænomener beregnes ved hjælp af formlen:

Z=U/I eller Z = R + J * (X_L -X_C)

Hvor: Z - impedans; R – aktiv belastning; x_L , x_C – induktiv og kapacitiv belastning; J - koefficient.

Seriel og parallel forbindelse af elementer

For elementer i et elektrisk kredsløb (sektion af et kredsløb) er et karakteristisk punkt en seriel eller parallel forbindelse.

Følgelig er hver type forbindelse ledsaget af et forskelligt mønster af strømflow og spændingsforsyning.I denne forbindelse anvendes Ohms lov også forskelligt, afhængigt af muligheden for at inkludere elementer.

Kredsløb af serieforbundne resistive elementer

I forhold til en serieforbindelse (en sektion af et kredsløb med to komponenter) anvendes følgende formulering:

• jeg = jeg₁ =I₂ ;
• U = U₁ +U₂ ;
• R = R₁ + R₂

Denne formulering viser tydeligt, at uanset antallet af resistive komponenter forbundet i serie, ændres strømmen, der flyder gennem en sektion af kredsløbet, ikke i værdi.

Forbindelse af resistive elementer i en sektion af kredsløbet i serie med hinanden. Denne mulighed har sin egen beregningslov. I diagrammet: I, I1, I2 - strømflow; R1, R2 - resistive elementer; U, U1, U2 - påført spænding

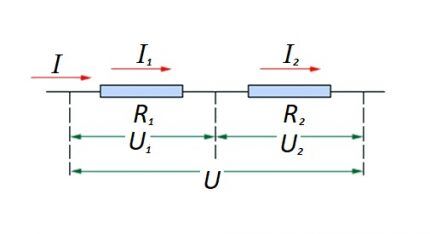
Størrelsen af ​​spændingen påført de effektive resistive komponenter i kredsløbet er summen og summerer værdien af ​​emk-kilden.

I dette tilfælde er spændingen på hver enkelt komponent lig med: Ux = I * Rx.

Den samlede modstand skal betragtes som summen af ​​værdierne af alle resistive komponenter i kredsløbet.

Kredsløb af parallelforbundne resistive elementer

I det tilfælde, hvor der er en parallel forbindelse af resistive komponenter, anses følgende formulering for rimelig i forhold til den tyske fysiker Ohms lov:

• jeg = jeg₁ +I₂ … ;
• U = U₁ = U₂ … ;
• 1/R = 1/R₁ + 1/R₂ + …

Muligheder for at skabe kredsløbssektioner af en "blandet" type, når der anvendes parallelle og serielle forbindelser, er ikke udelukket.

Forbindelse af resistive elementer på en sektion af et kredsløb parallelt med hinanden. For denne mulighed anvendes en anden beregningslov. I diagrammet: I, I1, I2 - strømflow; R1, R2 - resistive elementer; U er den leverede spænding; A, B - ind-/udgangssteder

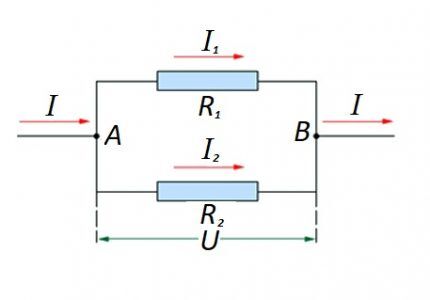
For sådanne muligheder udføres beregningen normalt ved indledningsvis at beregne modstandsværdien for parallelforbindelsen. Derefter tilføjes værdien af ​​modstanden forbundet i serie til det opnåede resultat.

Integrale og differentielle former for loven

Alle ovenstående punkter med beregninger gælder for forhold, når ledere af så at sige "homogen" struktur anvendes i elektriske kredsløb.

I mellemtiden er man i praksis ofte nødt til at beskæftige sig med opbygningen af ​​skemaer, hvor ledernes struktur ændres i forskellige sektioner. For eksempel anvendes ledninger med et større tværsnit eller omvendt et mindre, lavet af forskellige materialer.

For at tage højde for sådanne forskelle er der en variation af den såkaldte "differential-integral Ohms lov." For en infinitesimal leder beregnes strømtæthedsniveauet afhængigt af spændings- og ledningsevneværdien.

Følgende formel bruges til differentialberegning: J = ό * E

For integralberegningen er formuleringen derfor: I * R = φ1 – φ2 + έ

Imidlertid er disse eksempler temmelig tættere på skolen for højere matematik og bruges faktisk ikke i den virkelige praksis af en simpel elektriker.

Konklusioner og nyttig video om emnet

En detaljeret analyse af Ohms lov i videoen nedenfor vil hjælpe til endelig at konsolidere viden i denne retning.

En unik videolektion styrker kvalitativt den teoretiske skriftlige præsentation:

En elektrikers arbejde eller en elektronikingeniørs aktivitet er integreret forbundet med øjeblikke, hvor man faktisk skal overholde Georg Ohms lov i aktion. Dette er en slags truismer, som enhver professionel bør vide.

Omfattende viden om dette spørgsmål er ikke påkrævet - det er nok at lære de tre vigtigste variationer af ordlyden for at kunne anvende den i praksis.

Vil du supplere ovenstående materiale med værdifulde kommentarer eller give udtryk for din mening? Skriv venligst kommentarer i blokken under artiklen. Hvis du har spørgsmål, så tøv ikke med at spørge vores eksperter.